My PhD supervisor just won the Nobel prize in physics – here’s how his research on complex systems changed science

The Nobel Prize in Physics for 2021 has been jointly awarded to Italy’s Giorgio Parisi, Japan’s Syukuro Manabe and Germany’s Klaus Hasselmann for their “groundbreaking contributions to our understanding of complex systems”.

When I heard the news, I could hardly believe it. I studied for my master’s thesis and my PhD in theoretical physics under Professor Parisi at Sapienza University in Rome.

When I say I was in disbelief, don’t misunderstand me. Of all the people I’ve ever met in my research experience – perhaps in my life – he is without doubt the most ingenious. So I wasn’t surprised about the Nobel Prize committee’s decision to name him as a Laureate. Rather, it was their decision to recognise his “contributions to our understanding of complex systems” that piqued my interest.

This prize for Professor Parisi, split with trail-blazing meteorologists Professor Manabe and Professor Hasselmann, is an amazing recognition of an entire research area – perhaps a little less glamorous than the likes of general relativity or string theory – that attempts to understand and model what we in physics call “complex systems”.

These include things like climate ecosystems, financial systems, and biological phenomena, to name a few. The sheer variety of complex systems – represented in fluctuating markets and flocking starlings – makes it very hard to derive any sort of universal rules for them. Parisi’s work has allowed us to derive unprecedented conclusions about such systems that, on the surface, look random, unpredictable and impossible to model theoretically.

Unlike some other physics models, complex systems are not a collection of identical particles, regularly interacting in a way that is consistent and predictable. Instead, complex systems are systems of elements, potentially different from each other, interacting in different and seemingly unpredictable ways while exposed to varying external conditions.

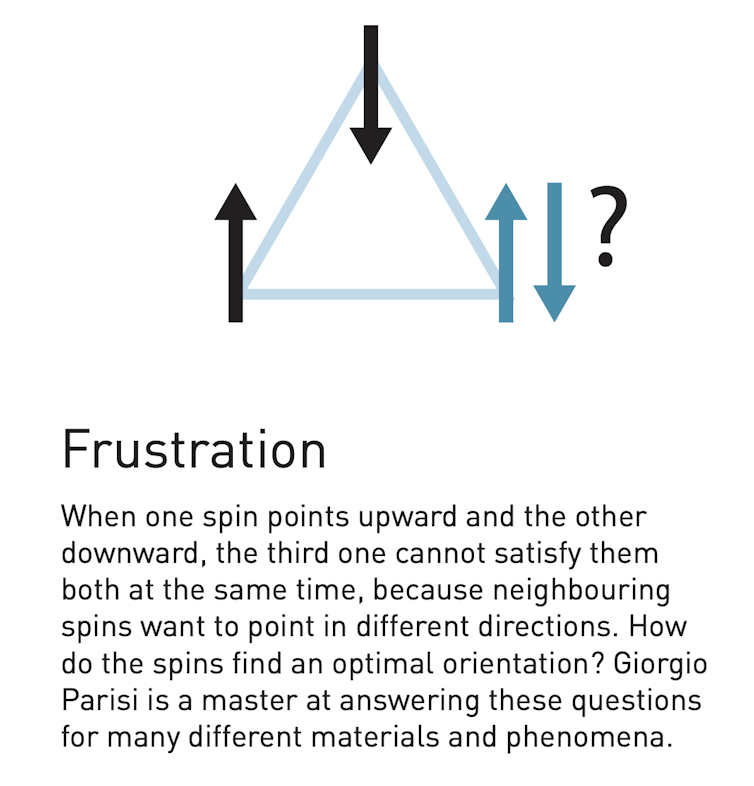
A stepping stone for modelling complex systems is the theory of “disordered systems”. These are essentially systems in which different pairs of elements experience different, potentially conflicting forces that can lead the elements to become “frustrated”.

A way of illustrating this is to imagine a party (a closed social system), where Alice may want to chat with Bob, and Bob may want to chat with Charlie, but Charlie may not want to chat with Alice. There’s frustration here – so what should they do?

Professor Parisi’s research clarified what happens when frustration occurs in disordered and complex systems. He identified that complex systems are able to remember their trajectories over time, and can get stuck in sub-optimal states for a long time.

In our party example, imagine Alice, Bob, Charlie, and other guests irregularly changing conversational groups and partners, hoping to find the best group of people to chat with – yet potentially never finding it. That’s the sub-optimal state complex systems can get stuck in.

Patterns from disorder

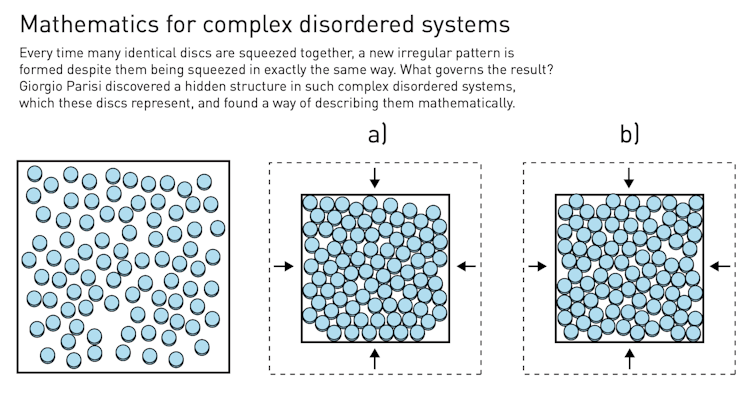
One of the many theoretical tools Professor Parisi has used to establish his theory is the so-called “replica trick” – a mathematical method which takes a disordered system, replicates it multiple times, and compares how different replicas of the system behave. You can do this, for instance, by compressing marbles in a box, which will form a different configuration each time you make the compression. Over many repetitions, Parisi knew, telling patterns might emerge.

This method is now one of the few theoretical pillars for the development of the whole theory of complex systems as we know it today. Professor Parisi’s theory has been shown to give reliable predictions on the statistical properties of complex systems ranging from supercooled liquids (liquids below their solidification temperature), frozen liquids, amorphous solids such as glass, and even flocks of starlings.

The theory of disordered systems allows us to make sense of the beautiful emergence of coherent flight patterns within tight flocks of birds – who manage to stick together and form vast groupings despite adverse conditions.

The same framework has been used to make sense of Earth’s climate. The meteorologists who share the Nobel prize with Professor Parisi will have relied upon breakthroughs in theoretical physics to produce the models we now use to reliably demonstrate global warming.

Read more:
Nobel prize: why climate modellers deserved the physics award – they’ve been proved right again and again

I had the chance to discuss these topics with Professor Parisi in Rome, while his experiments with flocks of birds were taking place and during his computer simulations on the behaviour of glass. Knowing a little of his mind, I am not at all surprised he has been awarded the Nobel prize in physics.

But I am pleasantly surprised that the field of complex systems, which is quietly pushing at the frontier of theoretical research in physics, has been given this exposure. This Nobel award has delivered new legitimacy – and, we can hope, new minds – to this fascinating area of contemporary physics.

Paolo Barucca does not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and has disclosed no relevant affiliations beyond their academic appointment.