Andrii Vodolazhskyi/Shutterstock
A year after the first cases of COVID-19 were found in China, mass vaccination programmes are now offering a chance to end the pandemic. At the same time, new strains, some of which appear to be more infectious than the original one, are threatening to derail progress in fighting the disease.
One way to capture the effectiveness of our effort to fight the virus is to consider the concept of “herd immunity”. During an epidemic, people become infected and those who survive usually become immune. Resistance to the disease can also be reached by vaccination, which complements the levels of natural immunity. Infected people increasingly come into contact with immune people rather than those who are still susceptible. Like a forest fire that runs out of dry wood, at the point of reaching herd immunity, the epidemic stops growing and starts to decline.
Mathematical models help us relate herd immunity levels to how fast the disease spreads. The percentage of immune people needed to create herd immunity depends on the reproductive number, R, which is a measure of how many people each infected person will infect on average. We can reach herd immunity either by waiting long enough so that large parts of the society pass through infection, by reducing the value of R using social distancing forever, or by vaccinating enough people.
Letting the epidemic run unchecked threatens to overload the health system and will result in many deaths. Conversely, lockdowns are causing economic, social and mental health issues. So we hope vaccines will stop the epidemic more effectively.
But how many people will need to be vaccinated to stop the disease spreading? This depends on how infectious the viral strain is, how effective the vaccine is, and how much we are prepared to continue with lockdown measures. The model predictions for the success of the vaccination programmes depend on the vaccine being able to limit the transmission of the virus – not just stop people getting ill. But we still don’t know if the current batch of approved COVID vaccines stops transmission.
Adam Kleczkowski
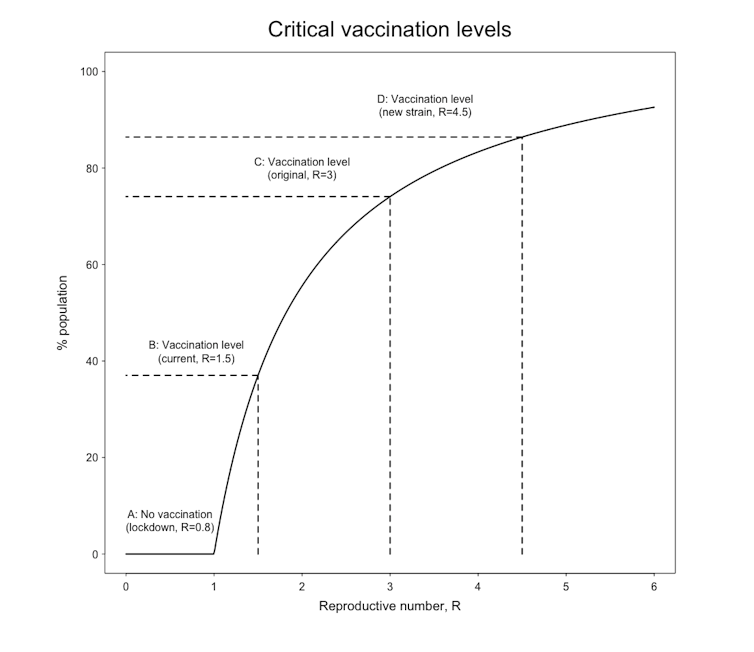
We could continue with very strict social distancing indefinitely, bringing R below 1 so that the number of new infections decreases. In this case, we would not need any vaccination (point marked A on the graph). But the moment control measures were relaxed, R would jump back above 1 and the epidemic would start to spread again.
Or we could combine some level of lockdown with the roll out of vaccines. In this scenario (point marked B on the graph) we would see a decline in cases once 40% of the population were immune to the virus. However, this strategy relies on keeping R just above 1. The disease would probably come back as soon as further relaxation occurred.
As we want to return to our activities and freedoms without social distancing, the vaccination levels need to be much higher, taking into account how fast the virus can spread with no additional control.
A reliable estimate of the rate of spread of the first variant of SARS-CoV-2, during the first stages of the epidemic, is R=3. In other words, every person infected with the coronavirus passes it on to three other people, on average. The corresponding herd immunity level for this value of R is 67%, so assuming a vaccine efficacy of 90%, we need to vaccinate 74% of the population (point marked C) to stop the virus from advancing further.
How does the emergence of the new variants change this value? We do not know for sure how fast the new strains would have spread if allowed to do so without any mitigation measures. The evidence suggests that the UK strain is 30-50%, and maybe as much as 70%, more infectious than the original one. Choosing the value of 50%, the needed vaccination levels are pushed up to 86% (point marked D).
An even higher proportion will need to be immunised if we want to push the virus towards eradication or to guard against a potential underestimation of the rate of spread.
Can such high levels of protection be attained at all? If a vaccine is only 50-70% effective, as the Oxford and Sinovac vaccines appear to be, this is the highest herd immunity level that can be achieved, if everybody gets the vaccine. Even with the higher efficacy of the Pfizer and Moderna vaccines, vaccinating nearly 90% of the population will be very difficult, as not everybody can or will want to be treated.
On the positive side, a previous COVID infection still provides good protection against reinfections and so we can probably count on nearly 20% of the population having natural immunity.
The herd immunity levels depend on R values and we can, to some extent, manipulate them by lockdowns. If countries can keep R reduced to just above 1, eradication can be achieved even with smaller vaccination levels. But what is really needed is a coherent long-term plan: one that includes both quick vaccination roll out and continuing social distancing and testing.
![]()
Adam Kleczkowski has received funding from BBSRC, NSF, Academy of Medical Sciences, and the Scottish Government.